Задача по математике

20 октября 2017

81.-90.        Дано комплексное число z. Требуется:

• записать число z в алгебраической, тригонометрической и показательной формах;
• найти все корни уравнения w³+z=0, изобразить эти корни на плоскости комплексной переменной.

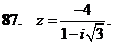
Решение.

1) Представим число  в алгебраической форме , где –действительная часть комплексного числа , а  – мнимая часть комплексного числа. Для этого умножим числитель и знаменатель дроби на число, сопряженное знаменателю  :

.

Итак,  — алгебраическая форма комплексного числа.

Тригонометрическая форма числа  имеет вид: , где  называется модулем комплексного числа , – аргумент комплексного числа. Тогда модуль и аргумент комплексного числа :

,

.

Итак,  — тригонометрическая форма комплексного числа.

Показательная форма:

.

Тогда: .

2) .

.

Представим число  в тригонометрической форме:

:

, .

Итак,  — тригонометрическая форма комплексного числа .

Для нахождения  воспользуемся формулой

, где .

В нашем случае имеем:

, k=0, 1, 2.

k=0: ;

k=1:

k=2:

Изобразим корни:

101.-110.              Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.

110. 110. а)                  б)      

в)       ;           г)      

Решение.

а)      

Под знаком предела есть иррациональность. Непосредственная подстановка предельного значения аргумента x= 2 приводит к неопределенности вида .

Чтобы раскрыть эту неопределенность, достаточно числитель и знаменатель дроби, стоящей под знаком предела, домножить на выражения сопряженные числителю и знаменателю дроби:

б)      

Воспользуемся тригонометрическими формулами:

в)       .